找准学生数学现实，促进知识有效迁移

 ———小学数学“小数的认识”课例研究

师大附小数学中低年级教研组执笔人：肖凌璇

数学知识本身是抽象的，但它又是寓于生活、扎根于现实的。毋庸置疑，在数学教学中，每位有经验的教师都会充分借助学生已有的生活经历和已有知识，使其发挥积极地迁移作用，来完成对新知识的学习。那么，是不是所有的生活经验都能对数学知识的学习产生正迁移呢？选用学生最熟悉的生活经验就是最好的选择吗？我们师大附小中低年级教研组决定围绕“找准学生数学现实，促进知识有效迁移”展开研究。吴老师执教的“小数的认识”（人教版义务教育课程标准实验教科书三年级下册）一课给我们提供了研究的开始。

上课前，教研组全体老师对吴老师的这节课进行了集备:由于小数的初步认识是在学生认识了万以内的数，会计算三位数的加减法，初步认识了分数，会计算简单的同分母分数加减法，并学习了常用计量单位的基础上进行的。小数对学生来说并不感到陌生，他们在商场、超市常会看到商品标价，而且在一年级下册学习“认识人民币”时，接触过小数。所以大家形成共识，决定用学生最熟悉的生活经验“元、角、分”计量单位的知识作为学习小数的形象支撑，并创设了较为丰富的，贴近儿童生活实际的情境，让学生在熟悉的情境中感悟小数的含义，与此同时在借鉴了高年级教研组的宝贵教研经验后决定对教研的形式做一些改变，听课的老师在听课的过程中有意识的从不同角度围绕此次教研的主题有侧重地观察这节课，分工如下：

教研活动负责人：陈淑兰 

教研主持人：肖凌璇   负责全课记录，课后研讨活动的主持及课例报告的整理

执教人：吴凌云老师

学生知识的前测、后测（课后对学生的访谈）黄莉及林惠老师

授课教师课堂语言、提问记录及分析   叶霞及林李晓老师

课堂学习中学生对老师问题的回答及分析 陈兢怡及方兰田老师

学生课堂学习状态记录（课堂的活动记录）  高晚钦及林玮老师

黄莉及林惠老师在上课前根据我们对课的设计进行了前测，根据结果进行了分析：

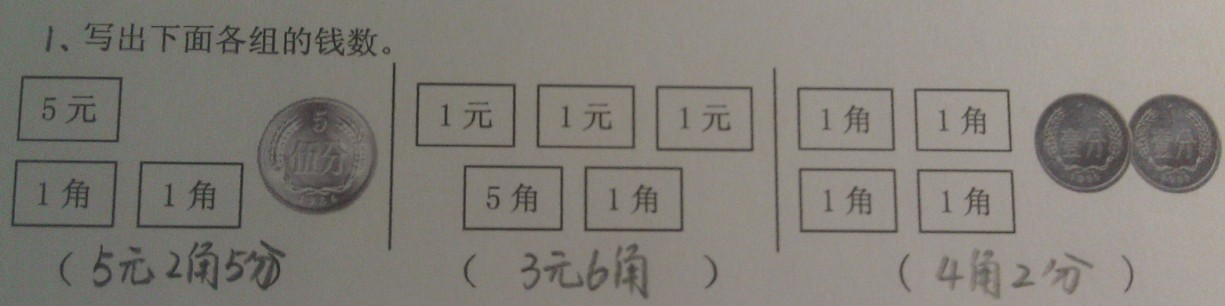
第一题：此次前测一共有32位学生参加，30位学生都是用元角分的形式来写的，只有2位学生会用小数的形式来表示上面的钱数。我们发现学生对于小数的熟悉程度远不如我们想象的那么好，学生看着小数说表示几元几角几分比较顺利，而反过来就不太顺利。

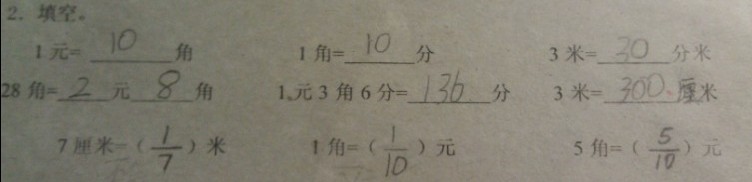
第二题：目的是了解学生对于我们学过的长度单位和元、角、分哪个更容易唤醒他们对小数的熟悉感。通过测试，发现75%的学生在把元角分换算成分数的形式中做全对，只有50%的学生会把厘米用分数的形式表示成几分之几米。据此我们认为在本课中使用人民币单位作为载体学习小数的认识比较符合学生的现实经验，更能促进学生知识的有效迁移。

之后我们中低年级教研组的全体数学老师一起观摩了吴老师的第一次授课:

……

师：把屏幕出现的钱数记录下来。生看图进行记录。投影展示：

1    7元；②6元4角；③3元2角1分；④7角5分。

（教师请生对钱的数量进行记录，结果只有一名学生会用小数记录，接下来教师完成了对小数读的教学。）

师：老师想请大家帮个忙。从1元钱里取出1角，怎么办？

（教师创设了一个请学生帮忙“从1元中取1角”的情境，用人民币单位作为载体学习小数的认识，并板书如下：

1角=元=0.1元        1分=元=0.01元

3角=元=0.3元        4分=元=0.04元

7角=元=0.7元        18分=元=0.18元

这个环节教师教的扎实，学生学的顺利。）

师出示米尺，PPT演示把米尺平均分成了10份。

师：1分米也可以用分数和小数来表示，你们会吗，是几？同桌商量一下。（学生迟疑不决）

师：1分米可以写成几分之几米？

生：1分米可以写成米。

师：怎么得到的？

生：1米=10分米，1米里有10个1分米，1分米就表示米。

师：小数呢？

生：0.01米。……（师进行了指导，告诉学生是0.1米，接下去完成了3分米和7分米的教学）

师出示100个小格的米尺图。

师：这里的1小格表示？

生：1厘米。

师：1厘米是几分之几米呢，跟你的同桌聊一聊。

师：用小数表示是什么？（课堂寂静，师一再鼓励）

生1：100.1米。……

生2：0.01米。

师：为什么是0.01米？（师再次进行了指导，用相同的方法完成了9厘米和24厘米的教学。板书如下：

1分米=米=0.1米       1厘米=米=0.01米

3分米=米=0.3 米       9厘米=米=0.09米

7分米=米=0.7米       24厘米= 米=0.24米）

…… 

师：下面各图的涂色部分能用0.3表示吗？为什么？

学生大部分都认为可以。教师提问：有没有不同意见？

     这时有一个学生说：不可以、

     师：为什么？

     生：如果3格是0.3，这里有9格就只有0.9了，所以不可以。

…… 

第一次课后教研组讨论：

课后讨论中，吴老师对自己的课并不满意也有许多困惑,这节课老师开始感觉挺顺的，可后来在长度单位时引导的很费力，每次好像都是要老师硬扭着孩子说出小数。

所有低中年级教研组老师观课后一起进行研讨。每位教师都从自己侧重观察的角度进行了分析：

叶霞及林李晓老师从授课教师课堂语言、提问方面进行了分析：

她们认为吴老师的教学充分借助学生们已有的生活经验——对元、角、分之间关系的认识出发，不断迁移出对小数的认识，这个过程水到渠成，自然而然。可是在教学长度单位中的小数含义时，师生配合比较牵强，学生对分数与小数的关系理解也不够透彻，以至于在找一位小数与分数的关系及后来的两位小数与分数的关系时，大部分学生理解的不是很到位。

陈兢怡及方兰田老师从课堂学习中学生对老师问题的回答进行了分析，她们认为在探究小数意义时，老师主要借助了货币单位这个具体的情境，从学生的回答中，我们发现在理解以元为单位的小数中，在教师的引导下，学生有了初步的认识，但是学生并没有很好地把元、角、分建立起的小数的模型类推到长度单位的学习上，在理解以米单位的小数意义时，还是存在着一定的困难。

高晚钦及林玮老师从学生课堂学习状态方面进行了分析，她们发现典型记录单如下：

从收上来的记录单来看仅有42%的同学在将整数的长度转换为以“米”为单位的小数和分数是完全正确的，为什么学生完成的不好，出现这些错误的原因在哪儿呢？她们分析认为把小数放在以“元”为单位的背景中来教学，学生容易接受，所以在货币单位的背景中学习似乎还挺顺利的，但同时学生的思维也被束缚了，只知道小数点后第一位表示角，第二位表示分，却忽视了小数的真正含义：十分之几可以用一位小数表示，百分之几可以用两位小数表示。

课后，我们对学生进行了访谈，发现学生对于用元做单位的小数表示几角和几分掌握的比较好，但是，学生对于分米、厘米与米之间怎样用分数和小数表示依然不理解，表示很困惑。从后测来看小数的知识没有很有效的得到迁移，学生对于用米作单位的小数表示分米和厘米依然存在障碍。

我们在集体反思和讨论时得到一个共识：本节课吴老师从学生们已有经验出发，出示多种人民币组合，以此引出小数写法，并揭示课题，教学小数的读法。接着从货币单位入手很容易就让学生迁移到小数的读写，课上教师成功利用分数的含义辅助迁移到小数含义的教学，这个过程教师进行了充分的扎实的教学。在接下来的环节中让学生感受长度单位中整数、小数和分数之间的关系，在这儿教师就发现学生不能如课前预设那样自主地去探究。当教师不得不把这部分知识用新授的方法进行教学的情况下，学生还学的很不理想……由此我们认为用人民币作学习材料是有局限的，借助元、角、分之间的关系并没有突破教学重难点，也就是说这节课未能抓准学生的现实经验，以致达不到促进知识的有效迁移。经过讨论，我们认为依然要从现实经验入手，但是需要更换一个载体进行教学。决定从学生另一个熟悉的生活经验“米、分米、厘米”计量单位的知识作为学习小数的形象支撑来学习小数的认识，期望能更容易达成教学目标。

在第一次上课之后，我们对要从哪个角度引出小数有了新的想法，于是我们对前测的题目进行了调整。

较第一次前测，我们给了学生2个连续的换算，看看学生对把长度的单位和元角分在同等条件下进行换算，哪个更容易想到。结果显示82%的学生会把元角分换算成小数的形式，但是分数形式的只有35%左右的学生会换算；66%的学生不知道长度单位的换算题要怎么入手。

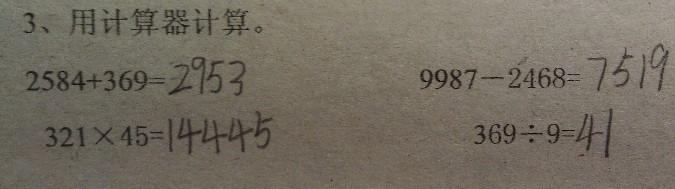
本题的目的是了解学生是否会使用计算器进行简单的计算，结果显示几乎所有学生都能正确使用。所以在本课中使用计算器进行教学的引入是没有问题的。      

这之后，吴老师开始了第二次授课：

（教师从小朋友喜欢的巧克力做促销引入，让生猜一猜一粒大约多少钱？在得不到整数结果的情况下让生用计算器进行操作，得到小数4.75，由此引出小数，之后完成了小数读及以元为单位小数具体含义的教学）

……

师：小青蛙跳的这个尺是1米高，把它平均分成10份，小青蛙跳一格是多少？

生：米

师：你是怎么看的？

生：1米长的尺子被平均分成了10份，每份是它的。

师：1分米就是米，刚才这个小朋友说得很好，把1米平均分成10份，，每份是，就是米。

师：写成小数……

生：0.1米

师：0.1米小数左边为什么是0？
生1：因为没有满1米。

生2：因为不到1米。

师：小数点右边的1表示什么？

生：表示分米。

(接下来3分米、7分米的教学先由学生自主探索，填写报告单，再由教师引导分析。)

师：小蜗牛也来了，它爬了（1厘米）。

（用相同的方法，教师完成了1厘米=米=0.01米的教学，3厘米、18厘米的写法教师放手了，让学生自行在学习单上进行填写，汇报显示学生能够独立写出。）

提高练习环节，学生在师出示人民币的时侯能够顺利写出以元为单位的3.21元，1.02元……

……

师：下面各图的涂色部分能用0.3表示吗？为什么？

 生：不可以。

师：为什么？

生：因为只平均分成了9分，涂色部分有3块，应该是3/9，不能写成0.3。

……

课后，黄莉老师对学生依然进行了访谈式的后测，“这节课你学会了什么？你知道为什么要使用小数吗？你喜欢小数吗？”有学生就体会到了小数是因为有些时候我们学过的整数或者分数已经无法表示某些数据，所以就必须使用到了新的数----小数。对于小数的意义不仅仅停留在元、角、分的固定格式上，还能理解一位小数和两位小数分别表示的意义。

访谈结束后，教研组的老师们再一次进行了讨论：

叶霞及林李晓老师认为经过锤炼，本节课教师的提问简洁、精炼，吴老师能依托有效情境提问，注重在教材的重点、难点处提问，在教材的重点处提问，重点就会突出；在难点处提问，难点就会突破。在对以元作单位的小数以及以米作单位的小数意义教学环节中，吴老师都会追问学生：“小数点左边第一位数表示什么？小数点右边第一位和第二位数分别表示什么？”小数的含义就是本节课的难点和重点，教师这样简洁的提问目标明确，就是要求学生认真思考，对学生清楚认识小数的含义有着重要作用，吴老师在教学中还能抓住时机，及时追问，促使知识深化。本节课中教师在这方面有多处体现。如：0.1米的小数点左边怎么是个0？3分米怎么能写成米呢？观察这些分数，你发现了什么等，进一步引导学生思考，使学生对知识的理解进一步深化。

陈兢怡及方兰田老师作了自己深入的分析：从引入部分的师生对话中我们可以了解到学生在生活中都已或多或少地接触过小数，所以对小数不会陌生。再者有了一些购物经验，所以对小数的读法以及在价格中所表示的含义也不会感到困难。在新课教学部分从孩子们的回答中我们发现学生已能较好的理解以米为单位的小数的实际含义，并且知道十分之几可以用一位小数表示，百分之几可以用两位小数表示。在我们最关注的那道辨析题中可以看出，通过本节课学习学生已能较深刻的理解了小数的意义。这些知识点的掌握正是因为教师能充分利用学生对基本单位长度以及对分数的认识作为学生的学习的起点。整个过程教师始终结合米、分米、厘米来开展学习活动，降低了学习难度，同时也方便了学生的理解。

高晚钦及林玮老师从从收上来的记录单看到有95%的同学在将整数的长度转换为以“米”为单位的小数和分数是完全正确的。充分说明利用长度作为学习的材料，在长度的基础上进行充分地建模，使得本节课课堂练习的完成情况比较理想。

第二部分，全体数学教师参与辨课。

会上老师们说了很多，各自表达了自己的观点。在辩课中大家形成了共识：本节课的伊始，吴老师的语言围绕求每一包巧克力单价展开，吴老师创设此情境用学生们已有的元、角、分的生活经验引入，有利于帮助学生们认识小数，读出小数，以及初步地理解小数的具体含义。再利用长度作为学习的材料，通过长度单位之间的改写来揭示分数和小数之间的这一本质联系，在长度的基础上进行充分地建模，使得本节课学生在理解一位小数表示十分之几、两位小数表示百分之几的知识点上有了突破。

我们的思考：小数的初步认识是小学生第一次真正意义上接触小数，是学生认数领域上的一次飞跃。从教材的知识结构来看，对于“小数的认识”主要分了两个阶段来学习。第一阶段是三年级下册结合长度单位及元角分来初步的认识小数；第二阶段安排在四年级上册系统的学习小数的意义。虽然学生对元、角、分的认识比长度单位更为熟悉，但是如果从元、角、分入手，孩子就会有固定思维，觉得小数就是按价格的格式，小数点前面表示元，小数点后第一位是角，第二位是分，完全的抛开了分数的意义，直接进行模仿。如果以长度单位为载体，再进一步教学小数的含义，从分数的意义迁移到小数，学生就会明白，其实分数就可以转化成小数，他们之间是互通的。

再思考：为什么以“米、分米、厘米”为主，辅以“元、角、分”计量单位等知识作为形象支撑来学习小数更容易突破重难点呢？

1．从认知的角度来讲，应该是从分数引出小数，利用人民币作材料来进行建模的话，往往是从小数引出分数，对孩子们来说十分之一元在生活中是没有见到过，我们分数的初步认识中是在一个物体或一个图形中平均分，而不是把十个独立的个体（1角）平均分，这应该是学习分数的意义的内容。从这点来看，用人民币作学习材料是有局限的。

2.长度来源于学生的生活现实，学生都有度量的经验。用长度作为材料，可以把一条一米长的线段平均分成10份，取其中的几份，即可以得到分数，学生能够很好地理解分数，顺着分数得出小数，然后再进行建模。在长度的基础上进行充分地建模，让学生发现分数与小数的联系，然后再让学生从小数发现分数，只要在学生建模的基础上得出人民币的分数即可。这样即为上面的学习进行了知识的巩固，也可以为下次学习分数的意义奠定好坚实的基础。

这次的课例研究给我们的启发：选用以元角分的货币单位为主要形象支撑来认识小数还是以米分米厘米的长度单位为主要形象支撑来认识小数呢？这是我们这个课例研究的重点。用测量物体的长度不能得到整数时，可以体现小数产生的必要性，而用元作单位，可能只是为了记录的简便,生活的需要。这次案例研究让我们深深体会到教材的情境选取是经过深思熟虑的。

我们不能脱离现实背景抽象地去学习小数,准确把握教学的起点，是确定教学目标和设计教学思路的关键。找准学生已有的现实经验和认知基础对于教学目标的实现是一项重要的课程资源。只有深入分析，不断尝试，才能真正找准学生数学现实，从而激活学生的相关生活经验和相关知识基础，以促进学习的正迁移，使学生在学会的同时，形成会学的能力。

                                      2012年12月